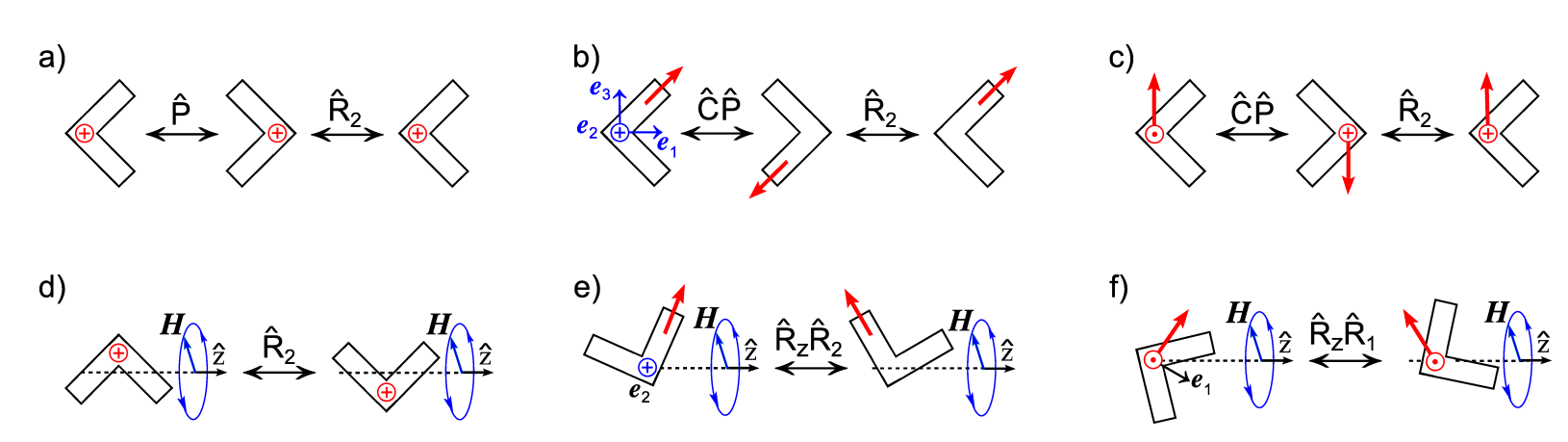
Schematic diagrams illustrating symmetries of a planar V-shaped object carrying a magnetic dipole moment (red) of different orientations with respect to parity, $\widehat{P}$, and charge conjugation, $\widehat{C}$. (a) $\widehat{P}$- (and $\widehat{C}\widehat{P}$-) even object; (b) $\widehat{C}\widehat{P}$-even (and $\widehat{P}$-odd) object; (c) $\widehat{C}\widehat{P}$- (and $\widehat{P}$-) odd object. Principal axes of rotation $\{\textbf{e}_1, \textbf{e}_2, \textbf{e}_3\}$ are shown in (b). (d-f) diagrams illustrating the pairs of solutions corresponding to (a-c).
Introduction and problem: Swimming at the micro scale is subject to low Reynolds (Re) number hydrodynamics. The scallop theorem dictates that any symmetric (time-reciprocal) motion cannot result in any net translation. Strictly, this symmetry requirement is only true in Newtonian fluids. We were the first to show that the scallop theorem can be overcome in non-Newtonian fluids [ ]. Nevertheless, all swimming microorganisms, such as bacteria or ciliates, have devised efficient schemes to break reciprocity in their motion and hence satisfy the scallop theorem. In artificial microsystems, however, one can apply external forces and torques, and then the scallop theorem no longer holds. For instance, a particularly powerful propulsion scheme at low Re is to rotate a propeller or drill akin to a bacterial flagellum using external fields and thus give rise to translation. This raises the question if a propeller has to be chiral to exhibit efficient rotation-translation coupling? Is it possible for highly symmetrical and achiral objects to propel, or does one need a corkscrew-propeller, which are commonly regarded to be the most efficient propellers? Surprisingly this fundamental question has thus far not been answered. The motivation is to find shapes that are simple to fabricate, yet propel well.
Our approach: Together with our collaborators at the Technion in Israel, we have just published a comprehensive analysis of the symmetries that underlie rotation-translation coupling [ ]. We fabricated V-shaped structures that possess a magnetic moment. The V-shape possesses two mutually orthogonal symmetry planes and is therefore highly symmetrical. We developed a cm-scale model as well as micron-sized structures (see Fig. 1a, b). The macroscopic model allowed us to precisely fix the orientation of the dipole moment with respect to the body. This is essential as the dipole orientation has important consequences on the symmetry and the associated propulsion gait of the object, a fact that has been overlooked in previous experimental studies. The micro-scale structure was fabricated using our unique glancing angle deposition (GLAD) technique. This also allowed us to fabricate V-shaped structures that are electrically polarizable (see Fig. 1c) and could therefore be driven with an electric instead of a magnetic field. This allowed us to identify the differences between the underlying symmetries and propulsion characteristics.

Figure 1: A cm-sized V-shape was fabricated via 3d printing (a), whereas micron-sized V-shapes where done with the GLAD technique (c, b). These structures are made of SiO2 and had either a ferromagnetic Nickel segment (white part in b) or one arm coated with gold (white part in c). The latter one could therefore be driven with an electric instead of a magnetic field.
Results: The first surprising result is that a highly symmetric V-shape can propel. Our rigorous symmetry analysis then shows – and this is the second surprising result – that a V-shape can be chiral! The latter is found when one correctly accounts for the symmetry of the magnetic moment in the structure. This has so far been overlooked in the literature. A truly remarkable result is that when an electric moment is used to rotate the structure, then the V-shape can propel even though it is achiral! For rotation-translation coupling to occur, the V-shape must precess around the external fields’ rotation axis. This is only possible, when the dipole moment is angled such that it does not rotate around one of the principal axes of rotation. As a result the V-shapes propulsion gait is critically dependent on the orientation of the dipole moment. This allowed us to drive the V-shape like a corkscrew propeller.
Discussion and Outlook: We describe the symmetry that is needed to propel a structure (microrobot) by rotation-translation coupling. We show that chirality is not a prerequisite and highly symmetrical shapes can be propulsive too. This allowed us to realize the first truly achiral propeller. This is useful as it allows one to identify simple shapes that can be used as propellers, including shapes that do not have to be chiral. We believe that this is important, because microfabrication of structures with high symmetry (including 2.5 D shapes) is generally easier than having to fabricate 3D chiral shapes. The work has been published in the journal Physical Review E [ ].

Figure 2: Displacement upon rotation in an external field plotted over time for two cm-sized V-shapes with different orientations of their magnetic dipole moment. While the upper object resembles the same propulsion gait as a corkscrew propeller (blue) the lower structure (red) rotates without notable net translational motion.
